One application of zero-knowledge proofs is that they allow protocols to be transformed from having possibly-malicious participants, who might not behave correctly, to honest-but-curious participants, who perform the protocol steps correctly, but might try to learn extra information.

To do this, each participant in the protocol constructs a zero-knowledge proof that they performed their step of the protocol correctly, then sends that proof along with the protocol message to their counterparty. The counterparty can verify the proof to check that the message was correctly computed, then proceed with their step, producing a proof that they performed their step correctly, and so on.

One observation about Merlin transcripts is that because proving and verification perform identical transcript operations, they perform the same transformation on an initial transcript state. This allows a duality between proving and verification behaviour: in the context above, each party can maintain their own transcript states, represented in the diagram by the two thick black lines. When one party proves that they performed their step correctly, they mutate the state of their transcript away from the state of their counterparty’s transcript.

But when the counterparty verifies the proof, the counterparty’s transcript state is mutated in the same way, bringing the two parties’ transcripts back into sync. Now the roles reverse, with the next proving phase mutating the transcript again, and the counterparty’s verification synchronizing the transcripts.

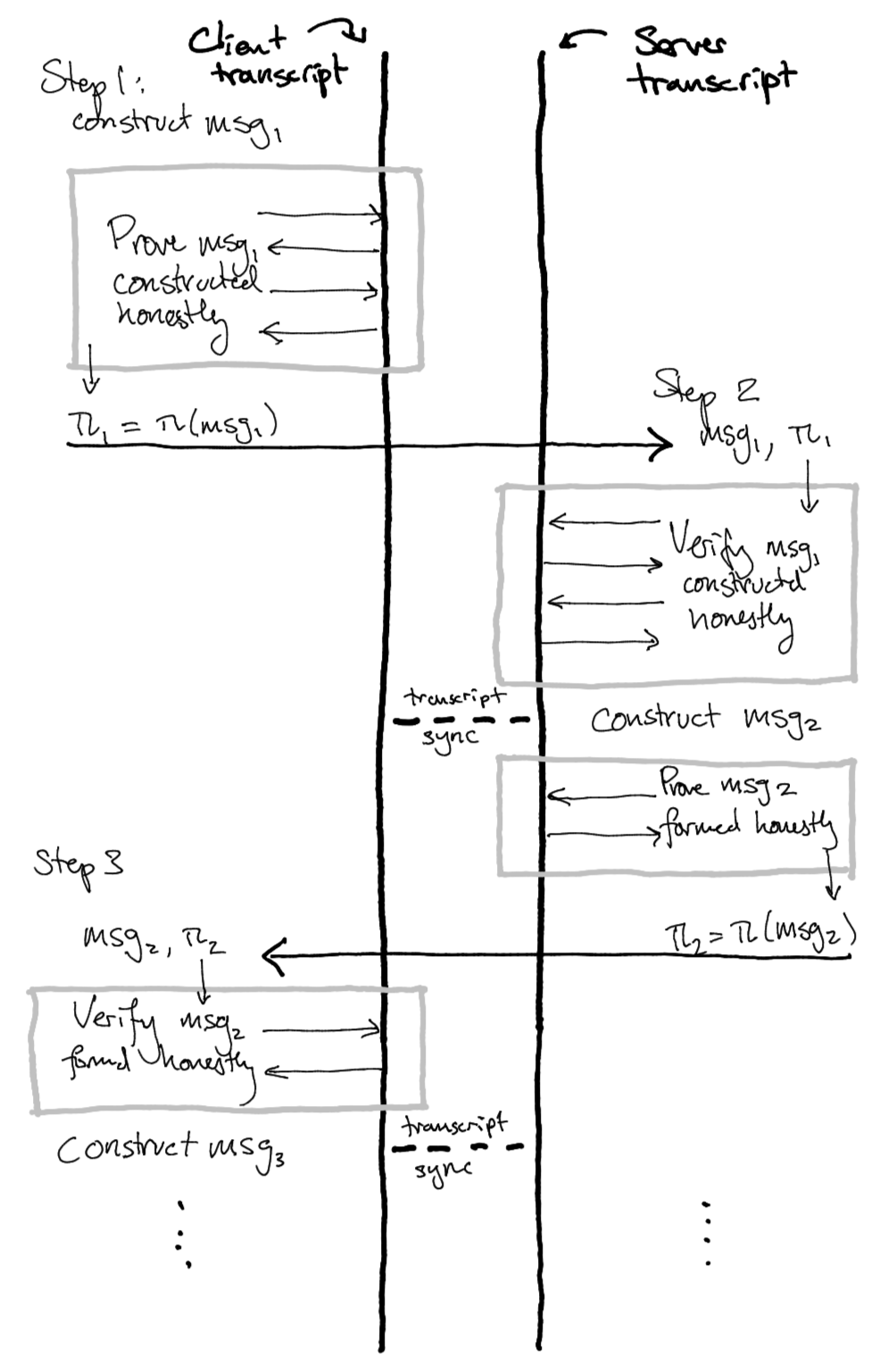
Notice that the proof of each step is a noninteractive proof, but because they’re made on the same transcript, they’re composed with all of the proofs from all prior steps, so it's not possible to replay an individual step's proof in a different context.

In this way, as the parties perform the protocol, they each also interactively compose the noninteractive proofs of correct execution of each step into a combined proof of correct execution of the entire protocol.