Merlin is a STROBE-based transcript construction for zero-knowledge proofs. It automates the Fiat-Shamir transform, so that by using Merlin, non-interactive protocols can be implemented as if they were interactive.

This is significantly easier and less error-prone than performing the transformation by hand, and in addition, it also provides natural support for:

• multi-round protocols with alternating commit and challenge phases;

• natural domain separation, ensuring challenges are bound to the statements to be proved;

• automatic message framing, preventing ambiguous encoding of commitment data;

• and protocol composition, by using a common transcript for multiple protocols.

Finally, Merlin also provides a transcript-based random number generator as defense-in-depth against bad-entropy attacks (such as nonce reuse, or bias over many proofs). This RNG provides synthetic randomness derived from the entire public transcript, as well as the prover's witness data, and an auxiliary input from an external RNG.

Merlin is authored by Henry de Valence, with design input from Isis Lovecruft and Oleg Andreev. The construction grew out of work with Oleg Andreev and Cathie Yun on a Bulletproofs implementation. Thanks also to Trevor Perrin and Mike Hamburg for helpful discussions. Merlin is named in reference to Arthur-Merlin protocols which introduced the notion of public coin arguments.

The header image was created by Oleg Andreev as a composite of Arthur Pyle's The Enchanter Merlin and the Keccak Team's θ-step diagram.

This project is licensed under the MIT license.

The Fiat-Shamir heuristic provides a way to transform a (public-coin) interactive argument into a non-interactive argument. Intuitively, the idea is to replace a verifier's random challenges with a hash of the prover's prior messages, but the exact details are usually unspecified.

Specifying these details requires deciding, among other things, what exactly the prover's messages are, how they are formatted, how to ensure the encoding is unambiguous, how to handle domain separators, how to link challenges between rounds (in the case of multi-round protocols), how to expand challenges (in the case that a protocol requires more challenge bytes than the digest size), etc.

More importantly, there's a conceptual gap: the protocols that people specify and analyze are interactive, while the protocols that people implement and use are non-interactive, and these related but distinct concepts are linked by an ad-hoc transformation left up to each proof system's implementor. This gap opens space for security vulnerabilities, such as in the Helios protocol used for IACR elections, and in the SwissPost/Scytl e-voting system.

In contrast, Merlin aims to fill this conceptual gap by providing an automatic linkage, handling the details of message framing and encoding, and allowing an implementation to be specified as if it were interactive, matching the description in a paper.

Merlin provides two objects: a transcript, which models the public interactions between a prover and a verifier, and a transcript RNG, which uses the transcript to provide defense-in-depth against bad entropy attacks.

This chapter describes how these objects are constructed and the operations they can perform:

• Transcript Operations describes the transcript object.

• Generating Randomness describes the transcript-based RNG.

The next chapter, Using Merlin, describes how to use Merlin to implement a proof protocol.

Merlin provides a specified way to use STROBE. STROBE is a protocol framework intended for constructing online transport protocols. Merlin is aimed at a different use-case, zero-knowledge proofs, so it uses only a subset of STROBE. This means that a Merlin implementation can either use a STROBE implementation as a library, or implement the required subset of STROBE operations directly. See the STROBE specification for more details on STROBE operations.

A Merlin transcript is a typed wrapper around a STROBE object, instantiated using Keccak-f/1600 at the 128-bit security level.

Merlin transcripts are initialized with a single parameter, app_label, a byte string which represents an application-specific domain separator. See the Passing Transcripts section for more details on usage.

To construct a Merlin transcript, first, construct a STROBE-128 object with the 11-byte label b"Merlin v1.0". Next, append the message body app_label with label b"dom-sep", as described in the following section. Finally, return the transcript.

Merlin messages are byte strings up to 4GB (u32::max_value() bytes) long. Very long messages are allowed but discouraged; consider prehashing long messages and appending the hash as a message. Messages are labeled by a byte string. See Transcript Protocols for more information about message labels.

To append a message message with label label, perform the STROBE operation

AD[label || LE32(message.len())](message);

where LE32(x) is the 4-byte, little-endian encoding of the 32-bit number x.

The notation OP[meta](data) is defined on page 9 of the STROBE paper. Because Merlin does not have a transport concept, the metadata is encoded using meta-AD.

To extract a sequence of challenge bytes labeled by label into the buffer dest, perform the STROBE operation

dest <- PRF[label || LE32(dest.len())]();

where LE32 is defined as before.

Merlin provides a STROBE-based RNG for use in proof implementations, which aims to provide a general defense-in-depth against bad-entropy attacks. It's intended to generalize from

1. the deterministic nonce generation in Ed25519 & RFC 6979;
2. Trevor Perrin's "synthetic" nonce generation for Generalised EdDSA;
3. and Mike Hamburg's nonce generation mechanism sketched in the STROBE paper;

towards a design that's flexible enough for arbitrarily complex public-coin arguments.

In Schnorr signatures (the context for the above designs), the "nonce" is really a blinding factor used for a single sigma-protocol (a proof of knowledge of the secret key, with the message in the context); in a more complex protocol like Bulletproofs, the prover runs a bunch of sigma protocols in sequence and needs a bunch of blinding factors for each of them.

As noted in Trevor's mail, bad randomness in the blinding factor can screw up Schnorr signatures in lots of ways:

• guessing the blinding reveals the secret;
• using the same blinding for two proofs reveals the secret;
• leaking a few bits of each blinding factor over many signatures can allow recovery of the secret.

For more complex ZK arguments there's probably lots of even more horrible ways that everything can go wrong.

In (1), the blinding factor is generated as the hash of both the message data and a secret key unique to each signer, so that the blinding factors are generated in a deterministic but secret way, avoiding problems with bad randomness. However, the choice to make the blinding factors fully deterministic makes fault injection attacks much easier, which has been used with some success on Ed25519.

In (2), the blinding factor is generated as the hash of all of the message data, some secret key, and some randomness from an external RNG. This retains the benefits of (1), but without the disadvantages of being fully deterministic. Trevor terms this "synthetic nonce generation".

The STROBE paper (3) describes a variant of (1) for performing STROBE-based Schnorr signatures, where the blinding factor is generated in the following way: first, the STROBE context is copied; then, the signer uses a private key k to perform the STROBE operations

KEY[sym-key](k);
r <- PRF[sig-determ]()

The STROBE design is nice because forking the transcript exactly when randomness is required ensures that, if the transcripts are different, the blinding factor will be different -- no matter how much extra data was fed into the transcript. This means that even though it's deterministic, it's automatically protected against an issue Trevor mentioned:

Without randomization, the algorithm is fragile to modifications and misuse. In particular, modifying it to add an extra input to h=... without also adding the input to r=... would leak the private scalar if the same message is signed with a different extra input. So would signing a message twice, once passing in an incorrect public key K (though the synthetic-nonce algorithm fixes this separately by hashing K into r).

Merlin provides a transcript-based RNG that combines the ideas from (2) and (3) above. To generate randomness, a prover:

1. creates a secret clone of the public transcript state up to that point, so that the RNG output is bound to the entire public transcript;

2. rekeys their clone with their secret witness data, so that the RNG output is bound to their secrets;

3. rekeys their clone with 32 bytes of entropy from an external RNG, avoiding fully deterministic proofs.

Binding the output to the transcript state ensures that two different proof contexts always generate different outputs. This prevents repeating blinding factors between proofs. Binding the output to the prover's witness data ensures that the PRF output has at least as much entropy as the witness does. Finally, binding the output to the output of an external RNG provides a backstop and avoids the downsides of fully deterministic generation.

In Merlin's setting, the only secrets available to the prover are the witness variables for the proof statement, so in the presence of a weak or failing RNG, the RNG's entropy is limited to the entropy of the witness variables.

A verifier can also use the transcript RNG to perform randomized verification checks, although defense-in-depth is less essential there. They can skip step 2, and perform only steps 1 and 3.

To rekey with secret witness bytes witness labeled by label, the prover performs the STROBE operations

KEY[label || LE32(witness.len())](witness);

To finalize the transcript RNG constructor into an RNG, the prover obtains rng, 32 bytes of output from an external rng, then performs

KEY[b"rng"](rng);

Ideally, the transcript, transcript RNG constructor, and transcript RNG should all have different types, so that it is impossible to accidentally rekey the public transcript, or use an RNG before it has been finalized.

The preceding chapter, Merlin Transcripts, describes how Merlin transcripts operate. This chapter describes how to use Merlin to implement a proof protocol:

• Transcript Protocols describes how to specify how a proof system's mathematical objects are encoded into transcript messages;
• Passing Transcripts describes how to pass transcripts into proving and verification functions, and how this can provide domain separation and sequential composition;
• Prover-Verifier Duality describes how two counterparties can interactively compose non-interactive proofs.

In general, a proof system operates on mathematical objects: finite field elements, elliptic curve points, etc., while Merlin provides a byte-oriented message API. This means that while Merlin handles the details of transcript hashing, message framing, and so on, it is the proof system implementation's responsibility to define its transcript protocol: how its mathematical objects (at the proof system layer) correspond to byte messages (at the Merlin layer).

This consists of two parts:

1. Defining a proof-specific domain separator and a set of labels for the messages specific to the protocol. The labels should be fixed, not defined at runtime, as runtime data should be in the message body, while the labels are part of the protocol definition. A sufficient condition for the transcript to be parseable is that the labels should be distinct and none should be a prefix of any other.

2. Defining how mathematical objects are encoded as bytes: for instance, how to encode a curve point as a byte string, or how to convert uniformly distributed challenge bytes to a uniformly-distributed scalar.

In Rust, a transcript protocol can be defined using an extension trait, to add the proof-specific behaviour to the library-provided Transcript type, as follows. Other languagues can accomplish the same task by other means:

# #![allow(unused_variables)]
#fn main() {
trait TranscriptProtocol {
    fn domain_sep(&mut self);
    fn append_point(&mut self, label: &'static [u8], point: &CompressedRistretto);
    fn challenge_scalar(&mut self, label: &'static [u8]) -> Scalar;
}

impl TranscriptProtocol for Transcript {
    fn domain_sep(&mut self) {
        // A proof-specific domain separation label that should
    // uniquely identify the proof statement.
        self.append_bytes(b"dom-sep", b"TranscriptProtocol Example");
    }

    fn append_point(&mut self, label: &'static [u8], point: &CompressedRistretto) {
        self.append_bytes(label, point.as_bytes());
    }

    fn challenge_scalar(&mut self, label: &'static [u8]) -> Scalar {
        // Reduce a double-width scalar to ensure a uniform distribution
        let mut buf = [0; 64];
        self.challenge_bytes(label, &mut buf);
        Scalar::from_bytes_mod_order_wide(&buf)
    }
}

#}

This provides a proof-specific domain separator function to mark the beginning of a proof statement, which should uniquely identify the proof statement, including any parameters. The example's functions leave the labels to the call sites in the rest of the implementation, allowing code like

# #![allow(unused_variables)]
#fn main() {
transcript.commit_point(b"A", A.compress());

#}

but it may be better to maintain a fixed set of labels internally to the definition of the transcript protocol.

The transcript protocol is also a convenient location to place validation logic for prover-supplied parameters, because if this validation logic is baked into the transcript protocol, it can't be accidentally omitted. For instance, a Schnorr proof may require that the prover-supplied points are not the identity element, and this logic can be included into a validate-and-append function.

Merlin models a proof proof protocol as operating on a transcript context. This means that implementations of proof protocols should not create a transcript internally, but accept an existing transcript as a parameter.

Because Merlin transcripts are passed as parameters to the proving and verification functions provided by a proof library, applications which use those library functions must create transcript objects to use those functions. But because the transcript creation function takes a domain separation label (see Transcript Operations), this means that every application using a Merlin-based proof system performs domain separation by default, as the application must supply a domain separation label.

Moreover, this also allows an application to bind a Merlin-based proof not just to a single label, but to arbitrary structured application data, by appending structured messages to a transcript before passing it to a proof function. For instance, an application can commit a message to a transcript to turn a Schnorr proof into a signature scheme.

Passing a transcript as a parameter also allows automatic sequential composition without requiring any changes to the implementations of the composed proofs. To compose two proof statements, a library or application can append a domain separator identifying the composition, pass the transcript to the first proof function, then pass the transcript to the second proof function. The second proof's messages and challenges are then bound to the first proof's, while the first proof's messages are bound to the composition declaration.

This can be used both at the application level, combining proofs from different libraries (for instance, combining a Bulletproof with a Schnorr proof), or at the library level, allowing a proof to be implemented internally as a composition of two proofs (for instance, implementing the inner-product proof in a Bulletproof independently from the range-to-inner-product reduction proof).

One application of zero-knowledge proofs is that they allow protocols to be transformed from having possibly-malicious participants, who might not behave correctly, to honest-but-curious participants, who perform the protocol steps correctly, but might try to learn extra information.

To do this, each participant in the protocol constructs a zero-knowledge proof that they performed their step of the protocol correctly, then sends that proof along with the protocol message to their counterparty. The counterparty can verify the proof to check that the message was correctly computed, then proceed with their step, producing a proof that they performed their step correctly, and so on.

One observation about Merlin transcripts is that because proving and verification perform identical transcript operations, they perform the same transformation on an initial transcript state. This allows a duality between proving and verification behaviour: in the context above, each party can maintain their own transcript states, represented in the diagram by the two thick black lines. When one party proves that they performed their step correctly, they mutate the state of their transcript away from the state of their counterparty’s transcript.

But when the counterparty verifies the proof, the counterparty’s transcript state is mutated in the same way, bringing the two parties’ transcripts back into sync. Now the roles reverse, with the next proving phase mutating the transcript again, and the counterparty’s verification synchronizing the transcripts.

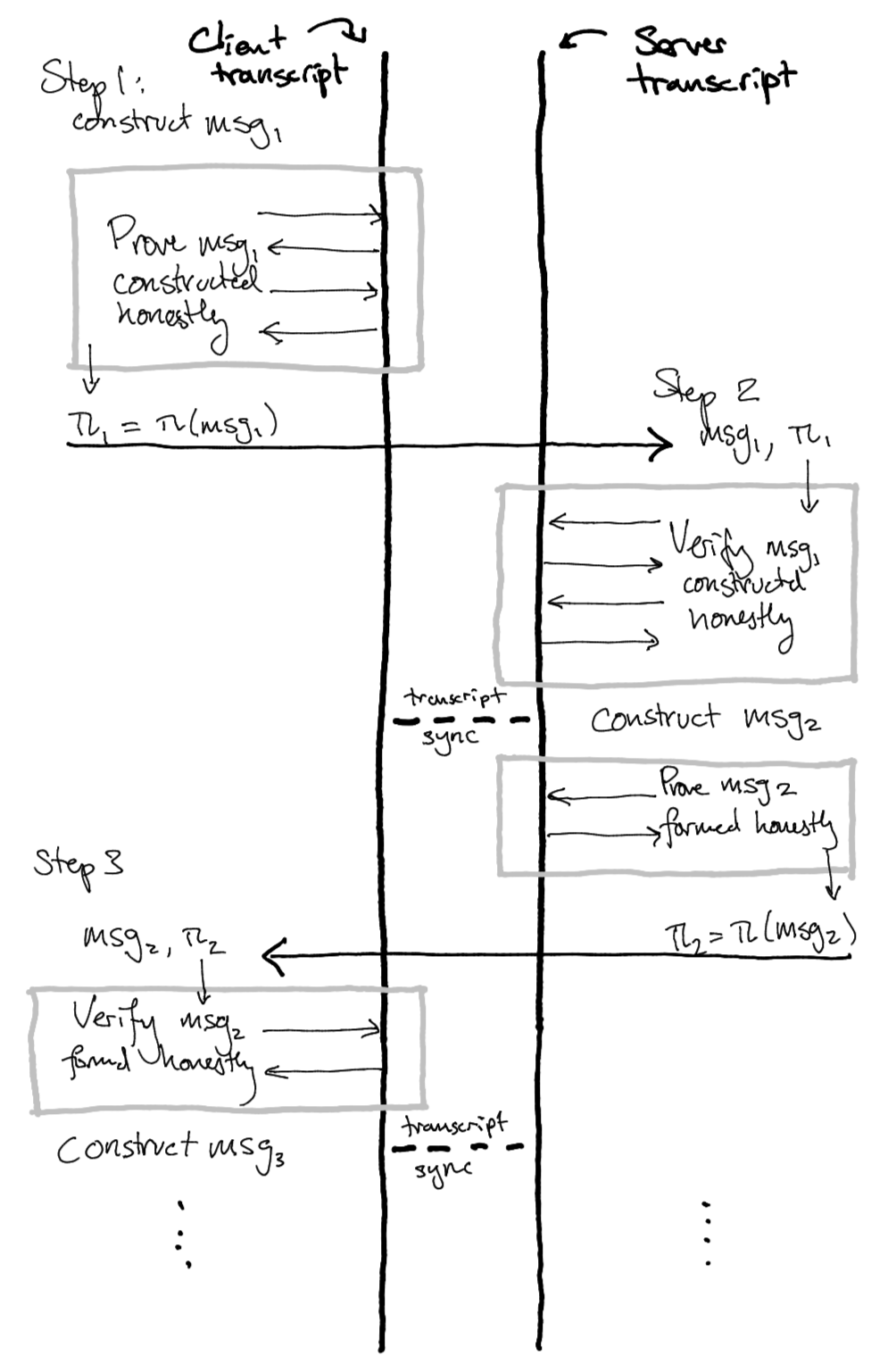
Notice that the proof of each step is a noninteractive proof, but because they’re made on the same transcript, they’re composed with all of the proofs from all prior steps, so it's not possible to replay an individual step's proof in a different context.

In this way, as the parties perform the protocol, they each also interactively compose the noninteractive proofs of correct execution of each step into a combined proof of correct execution of the entire protocol.

TBD (need to set up a CI deploy pipeline that auto-tests these)

To submit an addition to this list, submit a pull request on GitHub.

• merlin, the original Rust implementation. Stable.
• libmerlin, a single-file C implementation targeting C89. Feature-complete but unstable pending integration work.

To submit an addition to this list, submit a pull request on GitHub.

• dalek-cryptography Bulletproofs, a Ristretto-based Bulletproofs construction providing both range proofs and programmable constraint system proofs. Merlin transcripts allow constructing adaptive constraint systems with more efficient gadgets.

• dalek-cryptography zkp, a Ristretto-based toolkit for Schnorr proofs.

Merlin is feature-complete and the definitions of the transcript functions are stable.

It provides a single parameterization (using Keccak) aimed at software implementations. However, in the future, it would be interesting to provide a second parameterization (or family of parameterizations) aimed at use within a circuit, using a circuit-friendly sponge construction instead of Keccak.